High Performance Linear Algebra

Sam Halliday

Scala eXchange December 2014

https://www.youtube.com/watch?v=H8gXUaJMd3o

TL;DR

Four Decades of Free and Open Source Software, collaboration between industry and academia: high performance linear algebra (netlib), available in Scala (Breeze).
Not Invented Here: lukewarm performance, poor precision, dangerous results.

Linear Algebra

Definition

Linear algebra is a concept from pure mathematics which has been incredibly successful in applied mathematics, science and engineering.

Let's start from the abstract definitions to appreciate how large this field of research is.

(read slides)

Objects in a vector space do not need to be the vectors that you're probably thinking of: effectively an array of double numbers. They can be anything that meets these criteria and some of the rules of linearity imposed by Vector spaces. It is quite common for the "vectors" to be functions or polynomials.

Linear algebra starts when we have a Vector Space and is the launchpad for a wide variety of research topics in mathematics, such as: module theory, multilinear algebra, functional analysis, representation theory and algebraic geometry. Each with their own areas of application.

Is this familiar or is it alien? (Gauge audience understanding of linear algebra)

For anybody interested further in the theoretical side, I recommend Herstein's book "Topics in Algebra".

A Ring is a set with multiplication and addition.
A Field is a ring where multiplication is commutative ($a.b = b.a$) and nonzero elements have an inverse ($a.a^{-1} = 1$).
A Vector Space has elements from a Field (scalars) and a set (vectors) with vector addition ($v + m$) and scaling ($\alpha . b$)
A Basis of vectors ${v_1, v_2, \ldots, v_n}$ defines a coordinate system under which all other vectors can be represented: $a_1 v_1 + a_2 v_2 + \ldots + a_n v_n$
A Matrix encodes mappings between bases

Diagonalisation

$D = P^{-1} A P$
$D_{ij} = \delta_{ij}\lambda_i$
$AP = DP$
$A v_k = \lambda v_k$

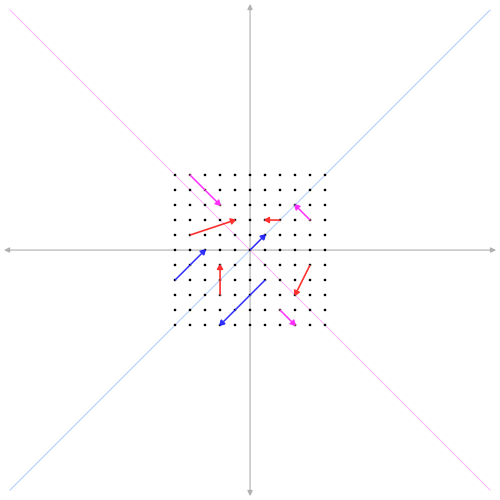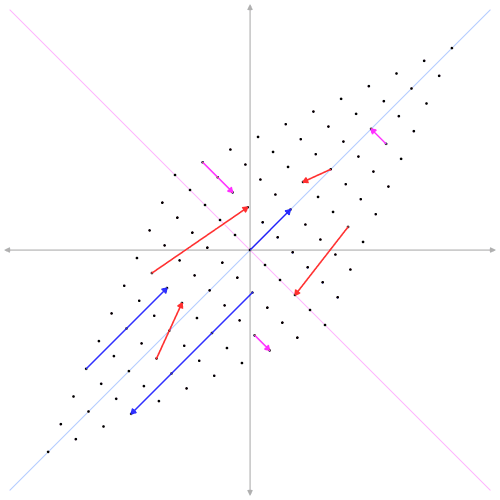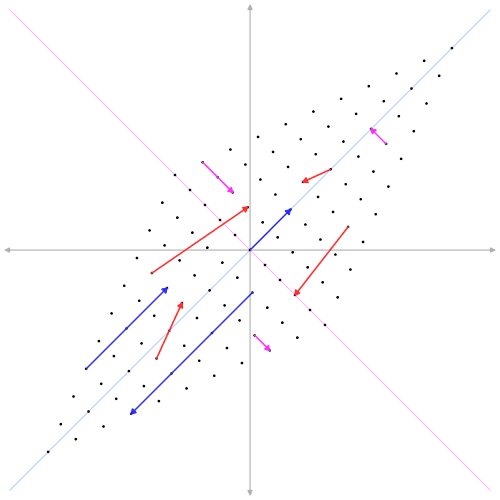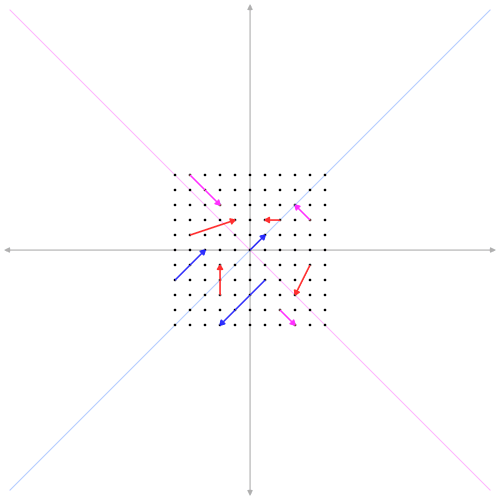
Example: Kalman Filter

\[ \mathbf{x}_{k} = \mathbf{F}_{k} \mathbf{x}_{k-1} + \mathbf{B}_{k} \mathbf{u}_{k} + \mathbf{w}_{k} \]

$\mathbf{x}_k$ is the state of the system at time slice $k$
$\mathbf{F}_k$ is the state transition model
$\mathbf{B}_k$ is the control-input model (applied to control vector $\mathbf{u}_k$)
$\mathbf{w}_k$ is the process noise, covariance $\mathbf{Q}_k$
observations $\mathbf{z}_k$ are made of the true state $\mathbf{x}_k$ according to
- $\mathbf{z}_k = \mathbf{H}_{k} \mathbf{x}_k + \mathbf{v}_k$
- $\mathbf{H}_k$ is the observation model and $\mathbf{v}_k$ is the observation noise (covariance $\mathbf{R}_k$)

Example: PCA

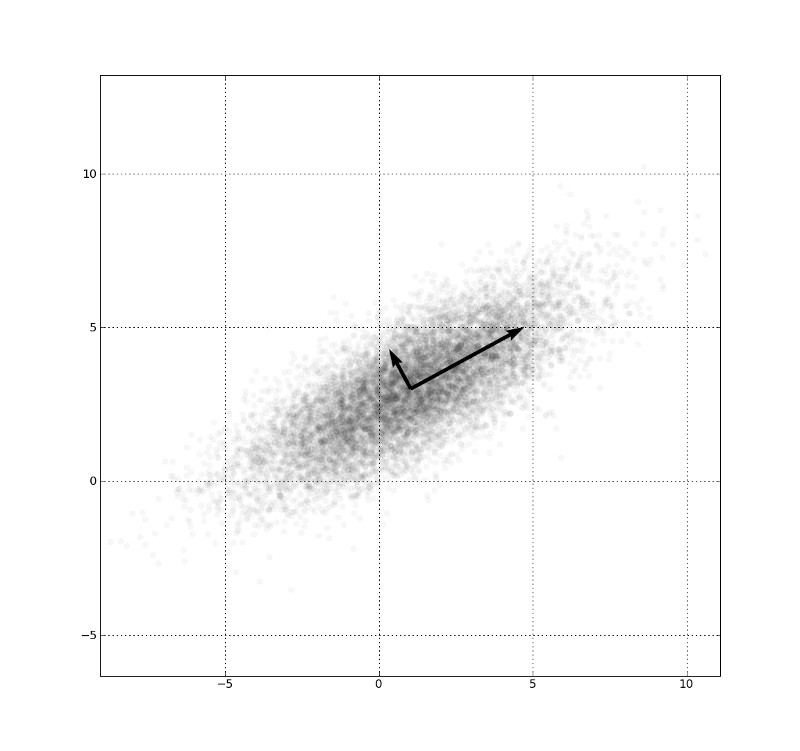
$\sigma_A^2 = \frac 1 n \sum_i^n a_i^2$
$\sigma_B^2 = \frac 1 n \sum_i^n b_i^2$
$\sigma_{AB}^2 = \frac 1 n \sum_i^n a_i b_i = \frac 1 n a b^T$

Data Matrix $X$
- all samples for one type of measurement per row
- different measure in each column
- all entries are diffs to the mean vector
$C_x = \frac 1 n X X^T$
$Y = PX$
$C_y = P C_x P^T$
find $P$ such that:
- $C_{ii}$ is maximised
- $C_{ij}$ is minimised $i \neq j$

\[ \begin{eqnarray*} C_y &=& P C_x P^T \\ &=& P P^{-1} D P P^T \\ &=& D \end{eqnarray*} \]

SVD

$X = U \Sigma V^T$
- $U$ is orthogonal (rotation)
- $\Sigma$ is diagonal (stretch)
- $V$ is orthogonal (rotation)
$XX^T = (U \Sigma V^T) (U \Sigma V^T)^T = U \Sigma^2 U^T$
$D^2 = C_y^2 = \Sigma$
$U = P$ (recall $Y = PX$)

Basic Implementation

Multiplication

\[ A=\begin{pmatrix} A_{11} & A_{12} & \cdots & A_{1m} \\ A_{21} & A_{22} & \cdots & A_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ A_{n1} & A_{n2} & \cdots & A_{nm} \\ \end{pmatrix} \qquad B=\begin{pmatrix} B_{11} & B_{12} & \cdots & B_{1p} \\ B_{21} & B_{22} & \cdots & B_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ B_{m1} & B_{m2} & \cdots & B_{mp} \\ \end{pmatrix} \]

\[ (A B)_{ij} = \sum_{k=1}^m A_{ik}B_{kj} \]

\[ \small \begin{pmatrix} \boldsymbol a & \boldsymbol b & \boldsymbol c \\ . & . & . \\ . & . & . \\ \end{pmatrix} \begin{pmatrix} \boldsymbol r & . & . \\ \boldsymbol u & . & . \\ \boldsymbol x & . & . \\ \end{pmatrix} = \begin{pmatrix} \boldsymbol \alpha & . & . \\ . & . & . \\ . & . & . \\ \end{pmatrix} \\[25pt] \begin{pmatrix} . & . & . \\ \boldsymbol d & \boldsymbol e & \boldsymbol f \\ . & . & . \\ \end{pmatrix} \begin{pmatrix} \boldsymbol r & . & . \\ \boldsymbol u & . & . \\ \boldsymbol x & . & . \\ \end{pmatrix} = \begin{pmatrix} . & . & . \\ \boldsymbol \delta & . & . \\ . & . & . \\ \end{pmatrix} \\[25pt] \begin{pmatrix} . & . & . \\ \boldsymbol d & \boldsymbol e & \boldsymbol f \\ . & . & . \\ \end{pmatrix} \begin{pmatrix} . & \boldsymbol s & . \\ . & \boldsymbol v & . \\ . & \boldsymbol y & . \\ \end{pmatrix} = \begin{pmatrix} . & . & . \\ . & \boldsymbol \epsilon & . \\ . & . & . \\ \end{pmatrix} \]

Immutable

  case class ImmutableMatrix(
    numRows: Int,
    numCols: Int,
    data: Vector[Vector[Double]]
  ) {
    def mult(that: ImmutableMatrix): ImmutableMatrix = {
      require(numCols == that.numRows)
      val res = Array.fill(numRows, that.numCols)(0.0)
      for {
        i <- 0 until numRows
        j <- 0 until that.numCols
        k <- 0 until numCols
      } {
        res(i)(j) = data(i)(k) * that.data(k)(j)
      }
      ImmutableMatrix(numRows, numCols, ImmutableMatrix.arrayToVec(res))
    }
  }

Naive

  trait Matrix {
    def numRows: Int
    def numCols: Int
    def set(row: Int, col: Int, value: Double): Unit
    def get(row: Int, col: Int): Double
    def mult(that: Matrix): Matrix
  }

  class NaiveMatrix (
    val numRows: Int,
    val numCols: Int,
    val values: Array[Array[Double]]
  ) extends Matrix {

    def set(row: Int, col: Int, value: Double): Unit =
      values(row)(col) = value

    def get(row: Int, col: Int): Double = values(row)(col)

    def mult(that: Matrix): Matrix = {
      val res = NaiveMatrix(numRows, that.numCols)
      for {
        i <- 0 until numRows
        j <- 0 until that.numCols
        k <- 0 until numCols
      } {
        val update = this.get(i, k) * that.get(k, j)
        res.set(i, j, res.get(i, j) + update)
      }
      res
    }
  }

Naive Parallel

  trait NaiveParallelMatrix {
    this: NaiveMatrix =>
    override def mult(that: Matrix): Matrix = {
      val res = NaiveMatrix(numRows, that.numCols)
      for {
        i <- (0 until numRows).par
        j <- (0 until that.numCols).par
        k <- 0 until numCols
      } {
        val update = this.get(i, k) * that.get(k, j)
        res.set(i, j, res.get(i, j) + update)
      }
      res
    }
  }

Allocation

http://github.com/fommil/lions-share

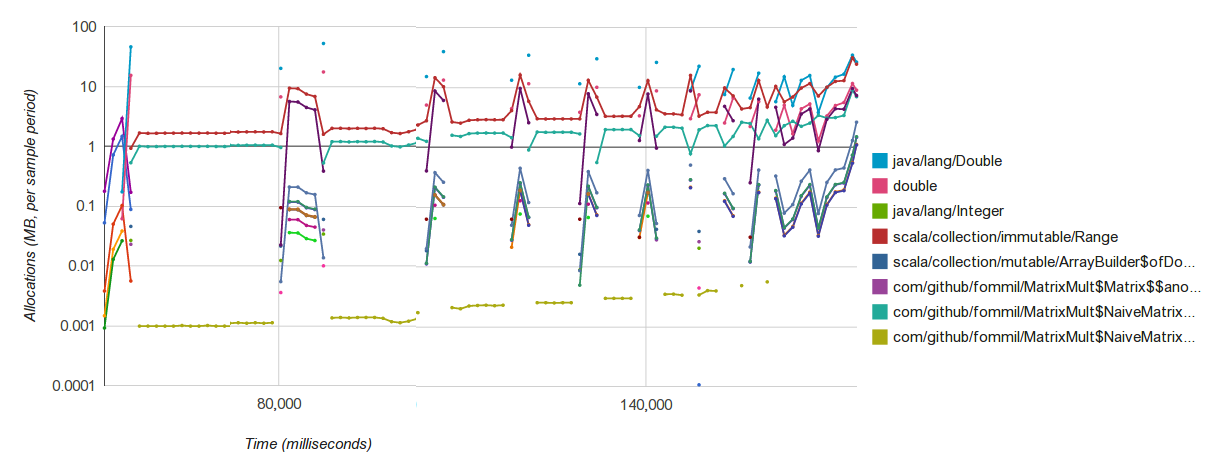
While Loops

  trait NaiveWhileMatrix {
    this: NaiveMatrix =>
    override def mult(that: Matrix): Matrix = {
      val res = NaiveMatrix(numRows, that.numCols)
      var i, j, k = 0
      while (i < numRows) {
        j = 0
        while (j < that.numCols) {
          k = 0
          var sum = 0.0
          while (k < numCols) {
            sum += this.get(i, k) * that.get(k, j)
            k += 1
          }
          res.set(i, j, sum)
          j += 1
        }
        i += 1
      }
      res
    }
  }

Comparison

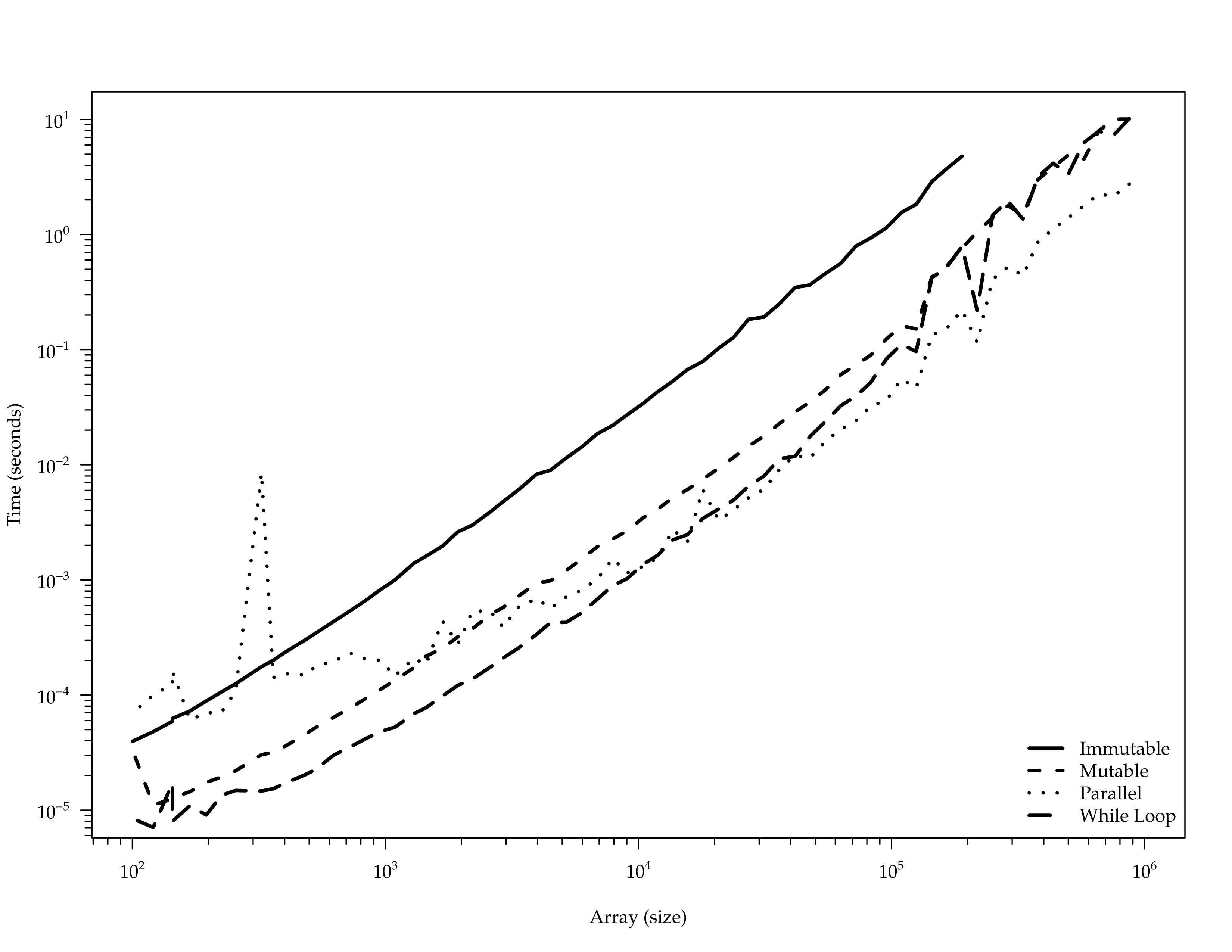
NETLIB

netlib.org

BLAS

Source: http://www.netlib.org/blas/blasqr.pdf

BLAS, short for "Basic Linear Algebra Subprograms" is a Fortran API split into three levels.

Level 1 contains vector operations on arrays: dot products, vector norms, a generalized vector addition of this form.

Level 2 was started in 1984 and published in 1988, containing matrix-vector operations including a generalized matrix-vector multiplication (GEMV), as well as a solver for $x$ when $T$ is triangular. The Level 2 subroutines are especially intended to improve performance of programs using BLAS on vector processors, where Level 1 BLAS are suboptimal because they hide the matrix-vector nature of the operations from the compiler.

Level 3 was formally published in 1990 and contains matrix-matrix operations, including a "general matrix multiplication" (GEMM), where A and B can optionally be transposed inside the routine. Also included are routines for solving B for triangular matrices T.

At least we now know the extent of our naivety: we tried to re-implement DGEMM.

Level	Name	Operation
1	`xAXPY`	$y \leftarrow \alpha x + y$
1	`xDOT`	$dot \leftarrow x^T y$
1	...
2	`xGEMV`	$y \leftarrow \alpha A x + \beta y$
2	`xTRSV`	$T \boldsymbol x = y$
2	...
3	`xGEMM`	$C \leftarrow \alpha A B + \beta C$
3	`xTRSM`	$T \boldsymbol B = \alpha \boldsymbol B$
3	...

Reference DGEMM

   *         Form  C := alpha*A*B + beta*C
             DO 90 J = 1,N
                  IF (BETA.EQ.ZERO) THEN
                      DO 50 I = 1,M
                          C(I,J) = ZERO
   50                 CONTINUE
                  ELSE IF (BETA.NE.ONE) THEN
                      DO 60 I = 1,M
                          C(I,J) = BETA*C(I,J)
   60                 CONTINUE
                  END IF
                  DO 80 L = 1,K
                      IF (B(L,J).NE.ZERO) THEN
                          TEMP = ALPHA*B(L,J)
                          DO 70 I = 1,M
                              C(I,J) = C(I,J) + TEMP*A(I,L)
   70                     CONTINUE
                      END IF
   80             CONTINUE
   90         CONTINUE

LAPACK

dbdsdc dbdsqr ddisna dgbbrd dgbcon dgbequ dgbequb dgbrfs dgbrfsx dgbsv
dgbsvx dgbsvxx dgbtrf dgbtrs dgebak dgebal dgebrd dgecon dgeequ
dgeequb dgees dgeesx dgeev dgeevx dgehrd dgejsv dgelqf dgels dgelsd
dgelss dgelsy dgeqlf dgeqp3 dgeqpf dgeqrf dgeqrfp dgerfs dgerfsx
dgerqf dgesdd dgesv dgesvd dgesvj dgesvx dgesvxx dgetrf dgetri dgetrs
dggbak dggbal dgges dggesx dggev dggevx dggglm dgghrd dgglse dggqrf
dggrqf dggsvd dggsvp dgtcon dgtrfs dgtsv dgtsvx dgttrf dgttrs dhgeqz
dhsein dhseqr dopgtr dopmtr dorgbr dorghr dorglq dorgql dorgqr dorgrq
dorgtr dormbr dormhr dormlq dormql dormqr dormrq dormrz dormtr dpbcon
dpbequ dpbrfs dpbstf dpbsv dpbsvx dpbtrf dpbtrs dpftrf dpftri dpftrs
dpocon dpoequ dpoequb dporfs dporfsx dposv dposvx dposvxx dpotrf
dpotri dpotrs dppcon dppequ dpprfs dppsv dppsvx dpptrf dpptri dpptrs
dpstrf dptcon dpteqr dptrfs dptsv dptsvx dpttrf dpttrs dsbev dsbevd
dsbevx dsbgst dsbgv dsbgvd dsbgvx dsbtrd dsfrk dspcon dspev dspevd
dspevx dspgst dspgv dspgvd dspgvx dsprfs dspsv dspsvx dsptrd dsptrf
dsptri dsptrs dstebz dstedc dstegr dstein dstemr dsteqr dsterf dstev
dstevd dstevr dstevx dsycon dsyequb dsyev dsyevd dsyevr dsyevx dsygst
dsygv dsygvd dsygvx dsyrfs dsyrfsx dsysv dsysvx dsysvxx dsytrd dsytrf
dsytri dsytrs dtbcon dtbrfs dtbtrs dtfsm dtftri dtfttp dtfttr dtgevc
dtgexc dtgsen dtgsja dtgsna dtgsyl dtpcon dtprfs dtptri dtptrs dtpttf
dtpttr dtrcon dtrevc dtrexc dtrrfs dtrsen dtrsna dtrsyl dtrtri dtrtrs
dtrttf dtrttp dtzrzf dsgesv dsposv

DGETRF

Let's just look at one of those methods, as an example of the amount of thought that has gone into this library. Take DGETRF, it computes the LU Decomposition of a matrix.

The LU Decomposition breaks a matrix into three, simpler, matrices. The Lower, the Upper and a diagonal matrix The theory behind why this is possible is absolutely beautiful and if you're interested further I strongly recommend Topics in Algebra by Herstein.

This is a graphical representation of the LU decomposition of a Walsh matrix, which has some applications in error correcting codes. So, DGETRF is able to produce L, U and P given an A.

Matrices of this L, U or P form are known as structured sparse, because their structure is known. From a practical point of view, the memory requirements are much lower than storing a full matrix. From a problem solver's point of view, some equations are known to be solvable when the matrices have particular forms.

\[ LP^{-1}U = A \]

Optional: Solving with LU

OPTIONAL: This is an optional mathematics slide, with an example of where LU decomposition can be used to solve a problem. Is there any interest in seeing this, or do you all know it already?

If we have a linear system $Ax = b$ where $A$ is a matrix, and $x,b$ are vectors, we'd like to calculate $x$ given $A$ and $b$.

We can calculate the LU Decomposition of $A$, remembering that $P$ is a diagonal matrix, and rearrange like so.

Then we solve for an intermediate vector $y$, before solving for $x$. The great thing about these two equations is that $L$ and $U$ are both triangular matrices, so we can use forward and back substitution like many of you may have learnt at high school.

Once the LU Decomposition has been calculated, many systems of this form can be solved efficiently.

$Ax=b$
$PA = LU$
$LUx = Pb$

$Ly = Pb$
$Ux = y$

\[ \begin{matrix} l_{1,1} x_1 & & & & & = & b_1 \\ l_{2,1} x_1 & + & l_{2,2} x_2 & & & = & b_2 \\ \vdots & & \vdots & \ddots & & & \vdots \\ l_{m,1} x_1 & + & l_{m,2} x_2 & + \dotsb + & l_{m,m} x_m & = & b_m \\ \end{matrix} \]

\[ x_1 = \frac{b_1}{l_{1,1}} \\ x_2 = \frac{b_2 - l_{2,1} x_1}{l_{2,2}} \\ x_m = \frac{b_m - \sum_{i=1}^{m-1} l_{m,i}x_i}{l_{m,m}} \\ \]

C API

In the GNU toolchain, Fortran's single-precision type maps into C float and double precision into double, which are consistent with the Java and Scala primitives of the same name.

But accessing the Fortran API from C is really nasty: there isn't even an official header file for blas.h so you don't even get parameter list checking. Instead, BLAS is accessed through the CBLAS API and LAPACK is accessed through LAPACKE. This allows C constructs to be used instead of magic characters. This is an example of what the CBLAS wrapper is doing.

It's worth noting that in Fortran, all input parameters are pointers. This is in contrast to C and Java where primitive types are copied when they are passed to a function. In Fortran, you pass a pointer to the primitive and it is always possible to update that primitive within your routine. Even more mutable than C and Java, what can go wrong?

#include "cblas.h"

void cblas_dgemm(const enum CBLAS_ORDER Order, const enum CBLAS_TRANSPOSE TransA,
                 const enum CBLAS_TRANSPOSE TransB, const int M, const int N,
                 const int K, const double alpha, const double  *A,
                 const int lda, const double  *B, const int ldb,
                 const double beta, double  *C, const int ldc) {
...
if( Order == CblasColMajor ) {
      if(TransA == CblasTrans) TA='T';
      else if ( TransA == CblasConjTrans ) TA='C';
      else if ( TransA == CblasNoTrans )   TA='N';
      else ...

      if(TransB == CblasTrans) TB='T';
      else if ( TransB == CblasConjTrans ) TB='C';
      else if ( TransB == CblasNoTrans )   TB='N';
      else ...

      #ifdef F77_CHAR
         F77_TA = C2F_CHAR(&TA);
         F77_TB = C2F_CHAR(&TB);
      #endif

      F77_dgemm(F77_TA, F77_TB, &F77_M, &F77_N, &F77_K, &alpha, A,
       &F77_lda, B, &F77_ldb, &beta, C, &F77_ldc);
   } else if (Order == CblasRowMajor) { ...

Precision and Stability

Kinds of Error

roundoff error
input error
machine precision: $\epsilon$

Types of Structures

Scalar, numbers, e.g. an eigenvalue
Vector, e.g. the solution $x$ of system $Ax=b$
Matrix, e.g. matrix inverse $A^{-1}$
Subspace, e.g. space spanned by eigenvectors

Relative Errors

$\hat{\alpha} \approx \alpha$
$\vert \hat{\alpha} - \alpha \vert$
$\vert \hat{\alpha} - \alpha \vert / \vert \alpha \vert$
$\vert \hat{\alpha} - \alpha \vert / \vert \hat{\alpha} \vert$
$10^{-5}\epsilon$ "5 decimal digits"

Norms

In order to measure the error in vectors and matrices, we need to measure their size, or more correctly its *norm*.

A simple norm to understand is the 1-norm, which simply adds up all the elements of a vector, or the largest column vector in a matrix.

The 2-norm is perhaps more intuitive for vectors, as it is the Euclidean metric, or Pythagoras. The equivalent for matrices is more complicated - and carries a non-trivial computational cost - so the Frobenius norm is usually substituted, although not at negligible cost.

The simplest of all norms is the magnitude of the largest component, the "infinity norm", which is understandable for vectors and matrices alike.

Thinking geometrically, the 1-norm is like considering the distance between two points in a city to be the distance that a taxi would drive between them on the city's traffic grid. The 2-norm would be "as the crow flies" and the infinity norm is like just remembering how far you have come North, South, East or West. However, such analogies can be misleading because there is nothing particularly special about the 2-norm that makes it universally more accurate.

Name	Vector	Matrix
1-norm	$\Vert x\Vert _{1} = \sum_i \vert x_i\vert$	$\Vert A\Vert _{1} = \max_j \sum_i \vert a_{ij}\vert$
2-norm	$\Vert x\Vert _2 = ( \sum_i \vert x_i\vert^2 )^{1/2}$	$\Vert A\Vert _2 = \max_{x \neq 0} \Vert Ax\Vert _2 / \Vert x\Vert _2$
Frobenius	$\Vert x \Vert_F = \Vert x \Vert_2$	$\Vert A\Vert _F = ( \sum_{ij} \vert a_{ij}\vert^2 )^{1/2}$
$\infty$ norm	$\Vert x\Vert _{\infty} = \max_i \vert x_i\vert$	$\Vert A\Vert _{\infty} = \max_i \sum_j \vert a_{ij}\vert$

Condition Number

\[ A = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 10 \end{array} \right) \qquad A^{-1} \approx \left( \begin{array}{ccc} -.667 & -1.333 & 1 \\ -.667 & 3.667 & -2 \\ 1 & -2 & 1 \end{array} \right) \]

\[\kappa_{\infty}(A) = 158.33\]

LAPACK RCOND(A) $\approx \frac 1 {\kappa_\infty}$

Example

Suppose we want to solve $Ax=b$. We can calculate the error in our solution for $x$ by querying netlib for the norm of $A$ with SLANGE and the reciprocal of $A$ with SGECON, multiplying by the machine error to get a bound on the error. We cheat and know the actual error, shown here for comparison.

But netlib also provides "expert" solvers, or drivers, which are much more accurate and can report on their error bound. Here, SGESVX, the expert equivalent, returns a more accurate solution with a smaller error bound.

There is ongoing research in the netlib community to come up with ever-more accurate solvers, and the main point I wanted to get across here was that this is something that is often overlooked by amateur implementations, but is absolutely critical to a wide range of applications. Not knowing your error bars can be disastrous.

\[ Ax = b \\ A = \left( \begin{array}{ccc} 4 & 16000 & 17000 \\ 2 & 5 & 8 \\ 3 & 6 & 10 \end{array}\right) \qquad b = \left( \begin{array}{c} 100.1 \\ .1 \\ .01 \end{array}\right) \]

ANORM = SLANGE( 'I', N, N, A, LDA, WORK )
CALL SGESV( N, 1, A, LDA, IPIV, B, LDB, INFO )
CALL SGECON( 'I', N, A, LDA, ANORM, RCOND, WORK, IWORK, INFO )
ERRBD = EPSMCH / RCOND

SGESV ERRBD $= 1.5\cdot 10^{-2}$
true error $= 1.5\cdot 10^{-3}$
SGESVX FERR $= 3.0 \cdot 10^{-5}$
true error $4.3 \cdot 10^{-7}$

Hardware Support

$y = a * x + b$

Mnemonic	Operands	Operation
VFMADD132SD	xmm,xmm,xmm/m64	$0=$0×$2+$1
VFMADD213SD	xmm,xmm,xmm/m64	$0=$1×$0+$2
VFMADD231SD	xmm,xmm,xmm/m64	$0=$1×$2+$0

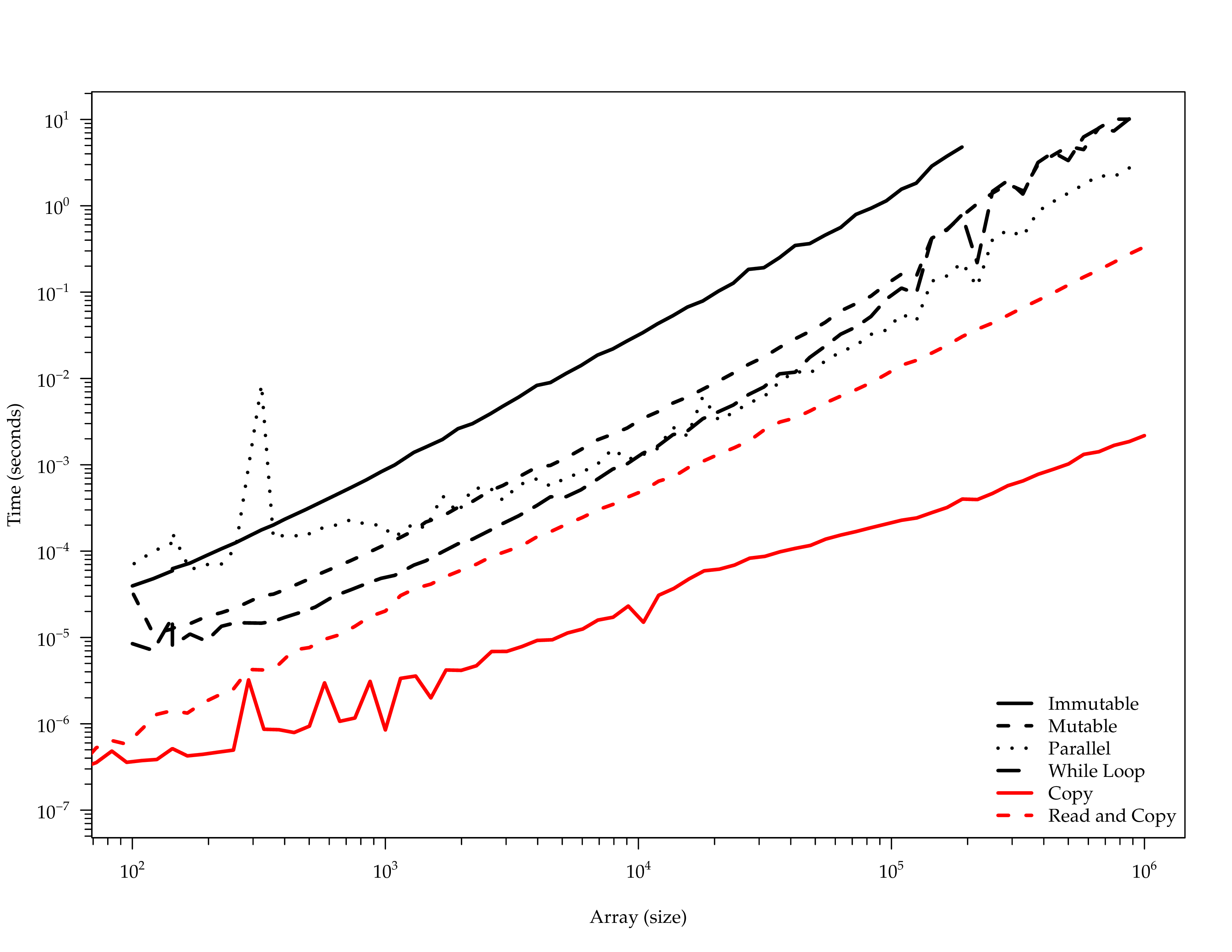
Bottleneck

Read and Write

    requestStart = currentTimeNanos();
    double* b = calloc(length, sizeof(double));

    for (i = 0 ; i < m ; i++) {
        c = i * m;
        for (j = 0 ; j < m ; j ++) {
            #ifdef READ_COL
            for (k = 0 ; k < m ; k++) {
                tmp = a[c + k];
            }
            b[c + j] = tmp;
            #else
            b[c + j] = a[c + j];
            #endif
        }
    }
    requestEnd = currentTimeNanos();

Timings

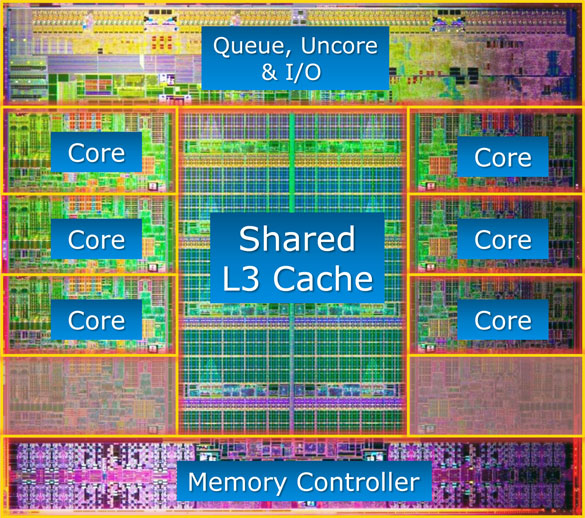
CPU Architecture

CPU Cycles

Source: http://en.wikipedia.org/wiki/X87#Performance
Source: http://stackoverflow.com/questions/15655835

This is a chart of some basic floating point operations on the x87 math co-processor, now part of the cores, bringing us up to about 2003.

If you've ever seen any numerical methods textbooks, you'll see lots of discussion around the order of magnitude of floating point operations, such as multiplication.

Those old textbooks are very much out of date. In the 1990s, a multiplication took slightly over 100 CPU cycles. In 2003, it took about 5 cycles, and nowadays multiple operations can happen in a single cycle. I've seen numbers that suggest Haswell does 32 floating point multiplications in a single cycle. That's an improvement of one in 5,000 cycles per operation (not even considering the improvements in clock speed).

I think we can safely say that counting multiplications has not been the bottleneck in linear algebra for a long time.

	FADD	FMUL	FDIV	FSQRT
80287	80	120	200	180
80387	30	45	90	125
80486	15	16	73	85
Pentium	2	2	39	70
Pentium II	2	4	25	35
Pentium 4	3	5	30	30
...	...	...	...	...
i7	$\frac 1 {32}$	$\frac 1 {32}$	$\frac 1 {32}$	$\frac 1 {32}$

Latency

Source: https://gist.github.com/hellerbarde/2843375#file-latency_humanized-markdown

The real bottleneck is moving data around: latency.

Peter Norvig once summarised common data access operations ordered by their timescale. His list is now somewhat out of date, but the relative timings have not changed much over the years.

To assist in understanding of the timescales, somebody multiplied all the times by a billion and related the tasks to things that we do as humans.

I've sanitised the examples a little bit to be more British.

The bottleneck we've seen is jumping between L1 and L2 cache references, and for much larger matrices (where a row cannot be held in L2), touching the main memory. For reference, my CPU has an L1 of 32k and an L2 of 256K.

Put in these terms, that means we're expecting somebody to read a book, but we keep asking them to go brush their teeth every time they finish a page.

Clearly, the most optimal solution will optimise the pipeline so that the L1 cache rarely misses.

Computer	Human Timescale	Human Analogy
L1 cache reference	0.5 secs	One heart beat
Branch mispredict	5 secs	Yawn
L2 cache reference	7 secs	Long yawn
Mutex lock/unlock	25 secs	Making a cup of tea
Main memory reference	100 secs	Brushing your teeth
Compress 1K bytes with Zippy	50 min	Scala compiler CI pipeline
Send 2K bytes over 1Gbps network	5.5 hr	Train London to Edinburgh
SSD random read	1.7 days	Weekend
Read 1MB sequentially from memory	2.9 days	Long weekend
Round trip within same datacenter	5.8 days	Short holiday
Read 1MB sequentially from SSD	11.6 days	Holiday
Disk seek	16.5 weeks	Term of university
Read 1MB sequentially from disk	7.8 months	Fully paid maternity in Norway
Send packet CA->Netherlands->CA	4.8 years	Government's term

Machine Optimised

Intel

You'll see in a moment, it's wipes the floor but really this slide summarises a practical consideration about the Intel implementation of BLAS.

This is a proprietary product, so we have no idea how they are doing anything.

It comes as part of a monolithic corporate package called Parallel Studio XE along with a bunch of other stuff that you probably don't need. And this is the price list as of November 2014.

The license does allow you to redistribute with your software, but you're looking at cluster licenses for every CI/QA/PROD box and either professional or composer licenses on DEV boxes.

Renewal prices in brackets.

However, if you speak to someone in Intel who knows about the products, they'll tell you that you can still buy the MKL standalone and it is a much more reasonable price. Honestly, if you do anything high performance, I think it's worth it. There is a tonne of other good stuff.

Parallel Studio

	Cluster	Professional	Composer
Named User	$2,949 ($1,049)	$2,299 ($799)	$1,449 ($499)
2 Floating Users	$14,749 ($5,199)	$11,499 ($4,049)	$5,099 ($1,799)
5 Floating Users	$29,499 ($10,349)	$22,999 ($8,049)	$10,899 ($3,849)

MKL Standalone

$499

AMD Core Math Library

Apple vecLib / Accelerate

$ ll /usr/lib/lib{blas, lapack}.dylib 
/usr/lib/libblas.dylib -> /System/Library/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
/usr/lib/liblapack.dylib -> /System/Library/Frameworks/vecLib.framework/Versions/A/libLAPACK.dylib

$ tree /System/Library/Frameworks/vecLib.framework/Versions/Current/
├── _CodeSignature
│   └── CodeResources
├── libBLAS.dylib
├── libLAPACK.dylib
├── libvDSP.dylib
├── libvMisc.dylib
├── Resources
│   ├── English.lproj
│   │   └── InfoPlist.strings
│   ├── Info.plist
│   └── version.plist
└── vecLib

ATLAS

The most well-known open source implementation of BLAS is ATLAS: Automatically Tuned Linear Algebra Software.

ATLAS relies heavily on compile-time analysis, which they call "automated empirical optimisation of software": ironically something can be solved using linear algebra. This means three main things, all involving compiling ATLAS lots of times:

compiling the same code with different compiler flags to see if there are any free wins.
compiling the same code with lots of different magic numbers to define things like cache edges and whether or not to copy matrices of various sizes.
trying out various different implementations of the same function, where there is no clear winner.
code generation of the level 3 BLAS and LAPACK routines to take all the above into account at the level of branches.

compiler flags - free wins
parameterisation
- cache edges - how much to attempt in kernels?
- copy - matrix data can be rearranged optimally
multiple implementations of the same function
- Fred's loop is faster than Bob's on your machine
code generation
- inline on steroids

cat /usr/share/doc/libatlas3-base/README.Debian

for A in /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor
  do sudo sh -c "echo performance > $A"
  done
cat /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor

sudo apt-get source atlas
sudo apt-get build-dep atlas
sudo apt-get install devscripts
cd atlas-*
fakeroot debian/rules custom
sudo dpkg -i ../libatlas*.deb

sudo update-alternatives --config libblas.so.3
sudo update-alternatives --config liblapack.so.3

GotoBLAS / OpenBLAS

$ ls OpenBLAS/kernel/x86_64/*dgemm*

dgemm_kernel_16x2_haswell.S     dgemm_kernel_6x4_piledriver.S
dgemm_ncopy_2.S dgemm_ncopy_8.S dgemm_tcopy_8_bulldozer.S
dgemm_kernel_4x4_haswell.S      dgemm_kernel_8x2_bulldozer.S
dgemm_ncopy_4.S dgemm_tcopy_2.S dgemm_tcopy_8.S
dgemm_kernel_4x8_sandy.S        dgemm_kernel_8x2_piledriver.S
dgemm_ncopy_8_bulldozer.S       dgemm_tcopy_4.S

DGEMM Benchmarks

requestStart = currentTimeNanos();
double* c = calloc(m * m, sizeof(double));
cblas_dgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, m, m, m, 1, a, m, b, m, 0, c, m);
requestEnd = currentTimeNanos();

LD_LIBRARY_PATH=. ./dgemmtest > ../R/netlib-ref.csv
LD_LIBRARY_PATH=/usr/lib/atlas-base ./dgemmtest > ../R/atlas.csv
LD_LIBRARY_PATH=/usr/lib/openblas-base ./dgemmtest > ../R/openblas.csv
LD_LIBRARY_PATH=/opt/acml5.3.1/gfortran64_mp/lib/:. ./dgemmtest > ../R/acml.csv
LD_LIBRARY_PATH=/opt/intel/mkl/lib/intel64:. ./dgemmtest > ../R/intel.csv

DGEMM Comparison

Here is the chart you've all been waiting for, overlaid on top of our Scala implementations. There is a lot of information here, so let's go through it slowly.

The Scala implementations are the black lines, same as before.

The red lines mark out the High Performance Zone that we discussed in the Bottleneck section.

The thick green line is the fortran reference implementation of blas. So the only real difference between this and the bottleneck discovery code is that it actually does the multiplications. We can really see that the time to do the multiplications is almost insignificant, as this is effectively sitting on the fence.

Let's then go into the open source implementations in green: ATLAS is good but OpenBLAS is leading the field.

We also get real performance gains from the proprietary implementations: AMD is in thick blue and Intel is below with blue dashes, and somewhere in between is the Apple implementation. Even though I run these a few times to allow warm-up, the proprietary implementations seem to have these spikes. I have no idea what they are: possibly poor handling of cases on cache boundaries.

It is truly remarkable that the optimised implementations take only a single order of magnitude more to do the work than to simply copy the arrays. And that's about a thousand times faster than our first attempt at a Scala implementation, and almost 100 times faster than the best we could come up with on the JVM.

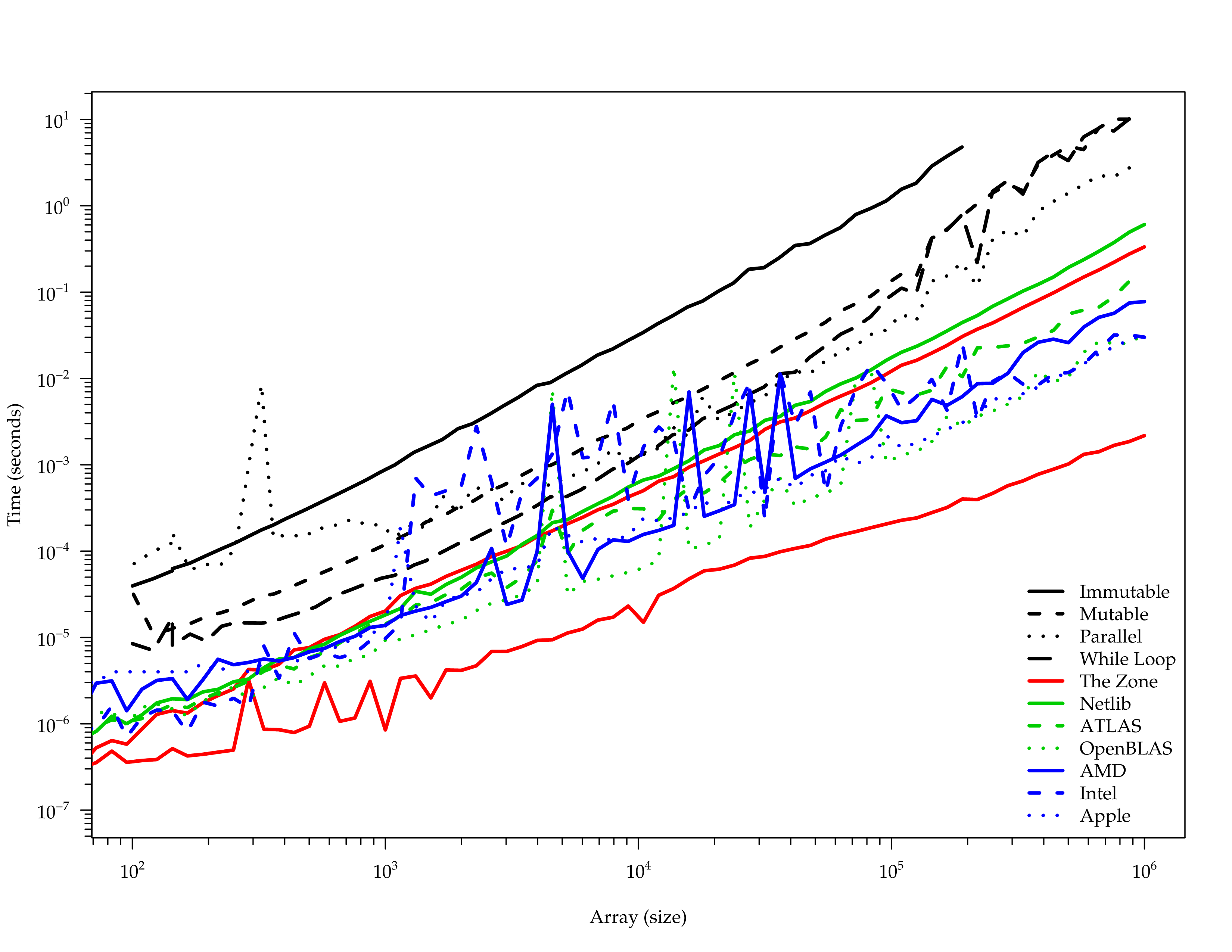
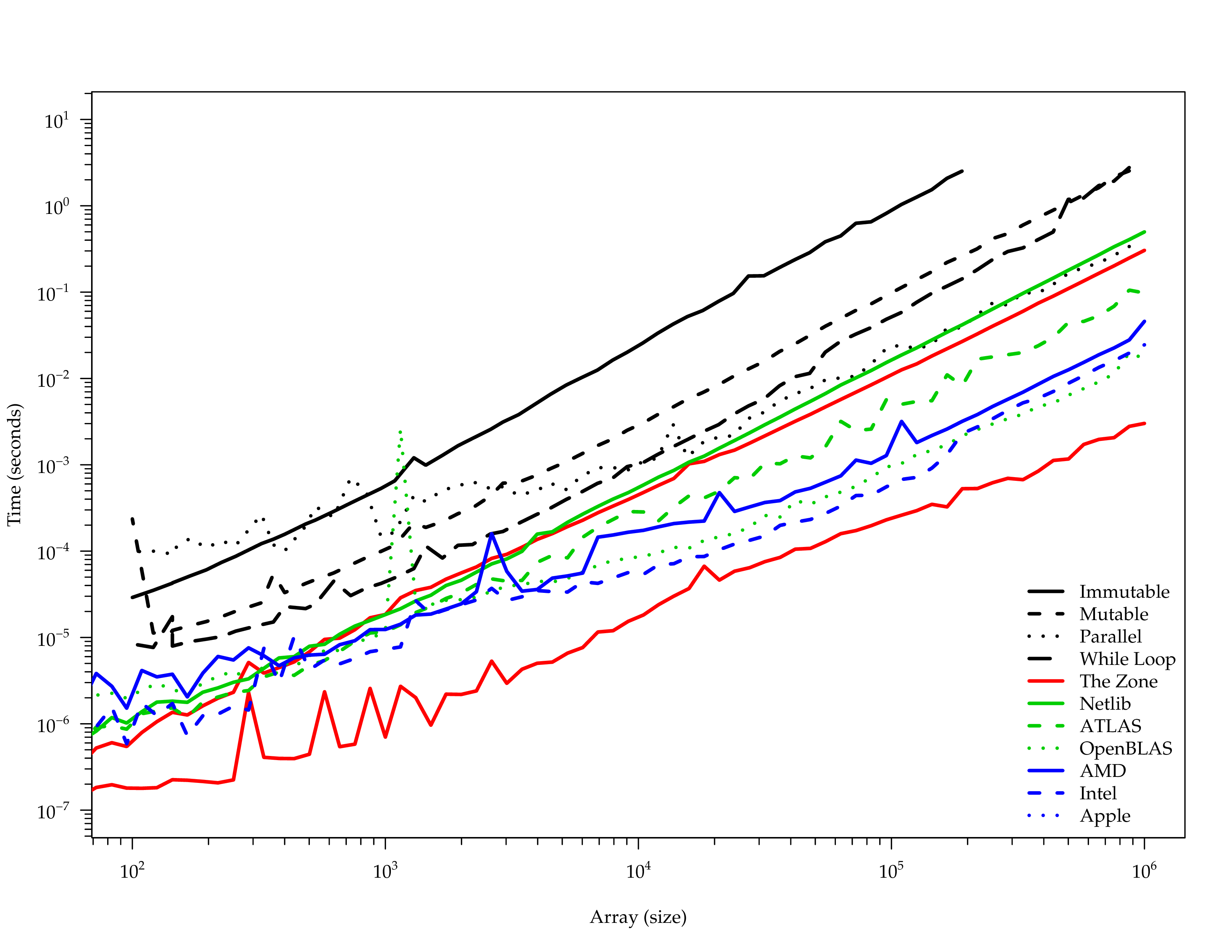
netlib-java

Fortran to ...

      IF( UPPER )THEN
         DO 70, J = 1, N
            DO 60, I = 1, M
               TEMP1 = ALPHA*B( I, J )
               TEMP2 = ZERO
               DO 50, K = 1, I - 1
                  C( K, J ) = C( K, J ) + TEMP1    *A( K, I )
                  TEMP2     = TEMP2     + B( K, J )*A( K, I )
50             CONTINUE
               IF( BETA.EQ.ZERO )THEN
                  C( I, J ) = TEMP1*A( I, I ) + ALPHA*TEMP2
               ELSE
                  C( I, J ) = BETA *C( I, J ) +
  $                           TEMP1*A( I, I ) + ALPHA*TEMP2
               END IF
60          CONTINUE
70       CONTINUE

... Java

Into Java, such as this.

There are a few things of particular note here. In Fortran, arrays are indexed from ONE --- as God intended. But obviously, in C and Java, the indexes start from zero, so there is a lot of plus/minus one going on.

The other thing is that Fortran likes to pass around pointers to parts of the array, but there is no way on the JVM to pass a reference to the middle of an array. You have to pass the full array and an offset/sublength. So that means there is a lot of boilerplate to deal with this.

Finally, Fortran 77 doesn't have loops and instead uses GOTO statements. For simple examples like this, loops are inferred and used, but in other parts of the code it is simply not possible to implement in Java, so Dummy.label is added at the various target points and a special Java processor is applied to construct JVM bytecode.

In fact, the production of the Java code itself is really a lie because the preferred behaviour of F2J is to compile straight to JVM bytecode.

if (upper) { 
  forloop70: for (j = 1; j <= n; j++) {
    forloop60: for (i = 1; i <= m; i++) { 
      temp1 = alpha * b[(i) - 1 + (j - 1) * ldb + _b_offset]; 
      temp2 = zero;
      forloop50: for (k = 1; k <= i - 1; k++) {
        c[(k) - 1 + (j - 1) * Ldc + _c_offset] = c[(k) - 1 + (j - 1) * Ldc + _c_offset] + temp1 * a[(k) - 1 + (i - 1) * lda + _a_offset];
        temp2 = temp2 + b[(k) - 1 + (j - 1) * ldb + _b_offset] * a[(k) - 1 + (i - 1) * lda + _a_offset];
        Dummy.label("Dsymm", 50);
      }
      if (beta == zero) {
        c[(i) - 1 + (j - 1) * Ldc + _c_offset] = temp1 * a[(i) - 1 + (i - 1) * lda + _a_offset] + alpha * temp2; 
      } else {
        c[(i) - 1 + (j - 1) * Ldc + _c_offset] = beta * c[(i) - 1 + (j - 1) * Ldc + _c_offset] + temp1 * a[(i) - 1 + (i - 1) * lda + _a_offset] + alpha * temp2;
      }
      Dummy.label("Dsymm", 60);
    }
    Dummy.label("Dsymm", 70);
  }
}

API Generator

abstract class BLAS {
  ...
  /**
   * ... original docs here ...
   */
  abstract public void dgemm(
    String transa,
    String transb,
    int m,
    int n,
    int k,
    double alpha,
    double[] a,
    int lda,
    double[] b,
    int ldb,
    double beta,
    double[] c,
    int Ldc
  );
  ...
}

Regex Digression

StringBuilder regex = new StringBuilder();
regex.append(format(">\\Q%s\\E</A></(?:B|strong)>\\(", name));
for (Class klass : types) {
  regex.append(format(
    ",?\\s*(?:<A[^>]+>)?[\\w.]*\\Q%s\\E(?:</A>)?(?:&lt;[^&]+&gt;)?&nbsp;([^),\\s]+)",
    klass.getSimpleName()
  ));
}
regex.append(format("\\)</CODE>"));

Pattern pattern = Pattern.compile(regex.toString(), MULTILINE | CASE_INSENSITIVE);
Matcher matcher = pattern.matcher(raw);

Implementations

F2jBLAS

@Override
public void dgemm(
  String transa, String transb, int m, int n, int k,
  double alpha, double[] a, int lda,
  double[] b, int ldb, double beta, double[] c, int Ldc
) {
 org.netlib.blas.Dgemm.dgemm(
   transa, transb, m, n, k, alpha, a, 0, lda, b, 0, ldb, beta, c, 0, Ldc
 );
}

NativeRefBLAS and NativeSystemBLAS

@Override
public native void dgemm(
  String transa, String transb, int m, int n, int k,
  double alpha, double[] a, int lda,
  double[] b, int ldb, double beta,
  double[] c, int Ldc
);

JNI

The Java Native Interface (JNI) implementation, which is auto-generated, looks something like this. I'd like to talk about some pitfalls with JNI.

There is a really nice third-party wrapper around native functions called JNA, but it has a major performance problem: it copies arrays both in and out of the native layer. And we know that's not great for performance.

But if we use standard JNI functions, and ask for ArrayPrimitive we'll also get a copy of the array. In order for the JNI code to be handed the actual array, as used in the JVM, we have to call CriticalArrayPrimitive.

But there is a problem with CriticalArrayPrimitive, once you call it, you potentially turn off the garbage collector. That could be a big problem if you are in a churn-heavy application and you're doing many of these operations.

But it's not as bad as it sounds. The reality is that the optimised native implementations make full use of your CPU, so there isn't much scope to do more than one of them at a time. Therefore, you're well advised to perform your higher level matrix operations in an Akka actor or in a synchronized block, to let the JVM have a bit of breathing room on either side to collect any garbage. This native code doesn't actually produce any garbage, but your code may do that while it's running.

If we wanted to avoid this problem, we could use NIO Buffers. But the problem with that is that it doesn't match onto the F2J implementation, so everyone living in pure JVM land will take the hit. Ideally, if I had an infinite amount of time to work on this, I'd rewrite F2J to use Buffers instead of arrays.

There are also some nasty implementation details to do with the exact size of primitives between C and JVM land, which means that not everything matches up nicely. Were you aware that the JVM represents int with a 64 bit C long long type? I've even seen people write --- shocking --- code in Scala to try and optimise heap usage, completely unaware of this fact.

JNIEXPORT void JNICALL Java_com_github_fommil_netlib_NativeSystemBLAS_dgemm (JNIEnv * env, jobject calling_obj, jstring transa, jstring transb, jint m, jint n, jint k, jdouble alpha, jdoubleArray a, jint lda, jdoubleArray b, jint ldb, jdouble beta, jdoubleArray c, jint Ldc) {
  char * jni_transa = (char *)(*env)->GetStringUTFChars(env, transa, JNI_FALSE);
  char * jni_transb = (char *)(*env)->GetStringUTFChars(env, transb, JNI_FALSE);
  jdouble * jni_a = NULL;
  if (a != NULL) {
    jni_a = (*env)->GetPrimitiveArrayCritical(env, a, JNI_FALSE);
    check_memory(env, jni_a);
  }
  jdouble * jni_b = NULL;
  if (b != NULL) {
    jni_b = (*env)->GetPrimitiveArrayCritical(env, b, JNI_FALSE);
    check_memory(env, jni_b);
  }
  jdouble * jni_c = NULL;
  if (c != NULL) {
    jni_c = (*env)->GetPrimitiveArrayCritical(env, c, JNI_FALSE);
    check_memory(env, jni_c);
  }
  cblas_dgemm(CblasColMajor, getCblasTrans(jni_transa), getCblasTrans(jni_transb), m, n, k, alpha, jni_a, lda, jni_b, ldb, beta, jni_c, Ldc);
  if (c != NULL) (*env)->ReleasePrimitiveArrayCritical(env, c, jni_c, 0);
  if (b != NULL) (*env)->ReleasePrimitiveArrayCritical(env, b, jni_b, 0);
  if (a != NULL) (*env)->ReleasePrimitiveArrayCritical(env, a, jni_a, 0);
  (*env)->ReleaseStringUTFChars(env, transb, jni_transb);
  (*env)->ReleaseStringUTFChars(env, transa, jni_transa);
}

Maven Native

<plugin>
    <groupId>org.codehaus.mojo</groupId>
    <artifactId>native-maven-plugin</artifactId>
    <configuration>
        <javahVerbose>true</javahVerbose>
        <javahClassNames>
            <javahClassName>com.github.fommil.netlib.NativeSystemBLAS</javahClassName>
        </javahClassNames>
        <compilerStartOptions>
            <compilerStartOption>-O3</compilerStartOption>
        </compilerStartOptions>
        <sources>
            <source>
                <directory>${project.build.directory}/netlib-native</directory>
                <includes>
                    <include>*.c</include>
                </includes>
...

JNILoader

public class NativeSystemBLAS extends com.github.fommil.netlib.F2jBLAS {
  static {
    String jnilib = com.github.fommil.jni.JniNamer.getJniName("netlib-native_system");
    String natives = System.getProperty("com.github.fommil.netlib.NativeSystemBLAS.natives", jnilib);
    com.github.fommil.jni.JniLoader.load(natives.split(","));
  }
...
}

Performance

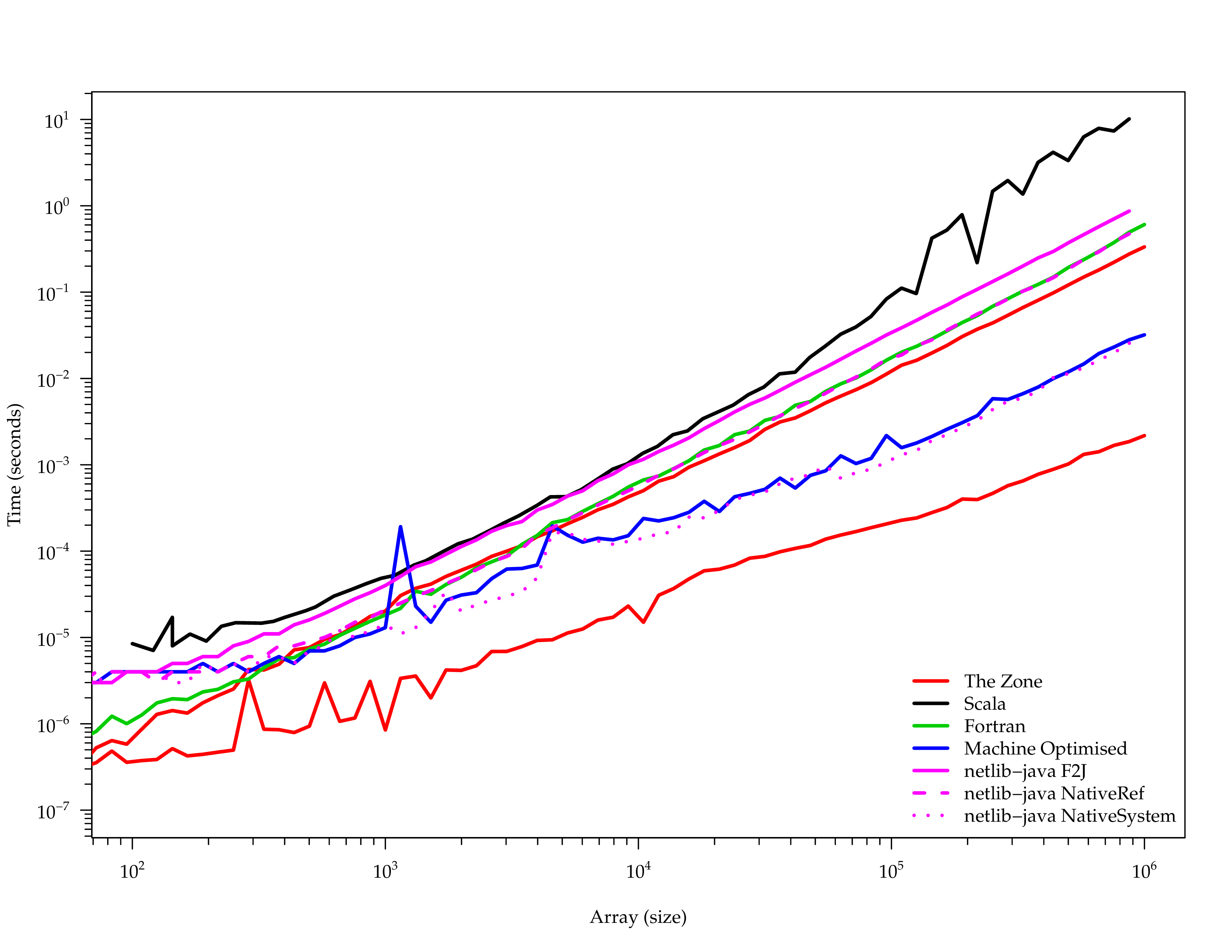
Scala API

Breeze

libraryDependencies ++= Seq(
  "org.scalanlp" %% "breeze" % "0.10",
  "org.scalanlp" %% "breeze-natives" % "0.10"
)

Nov 30, 2014 6:42:51 PM com.github.fommil.jni.JniLoader liberalLoad
INFO: successfully loaded /tmp/jniloader7150057786941522144netlib-native_system-linux-x86_64.so

scala> import breeze.linalg._

scala> val x = DenseVector.zeros[Double](5)
x: DenseVector[Double] = DenseVector(0.0, 0.0, 0.0, 0.0, 0.0)

scala> x.t
res1: Transpose[DenseVector[Double]] = Transpose(DenseVector(0.0, 0.0, 0.0, 0.0, 0.0))

scala> val m = DenseMatrix.zeros[Int](5,5)
m: DenseMatrix[Int] = 
0  0  0  0  0  
0  0  0  0  0  
0  0  0  0  0  
0  0  0  0  0  
0  0  0  0  0  

scala> (m.rows, m.cols)
(Int, Int) = (5,5)

scala> m(::,1)
DenseVector[Int] = DenseVector(0, 0, 0, 0, 0)

scala> m(4,::) := DenseVector(1,2,3,4,5).t
DenseMatrix[Int] = 1  2  3  4  5 

scala> m
DenseMatrix[Int] = 
0  0  0  0  0  
0  0  0  0  0  
0  0  0  0  0  
0  0  0  0  0  
1  2  3  4  5

Operation	Example
Elementwise addition	a + b
Elementwise multiplication	a :* b
Vector dot product	a dot b
Elementwise sum	sum(a)
Elementwise max	a.max
Elementwise argmax	argmax(a)
Linear solve	a b
Transpose	a.t
Determinant	det(a)
Inverse	inv(a)
Pseudoinverse	pinv(a)
SVD	SVD(u,s,v) = svd(a)

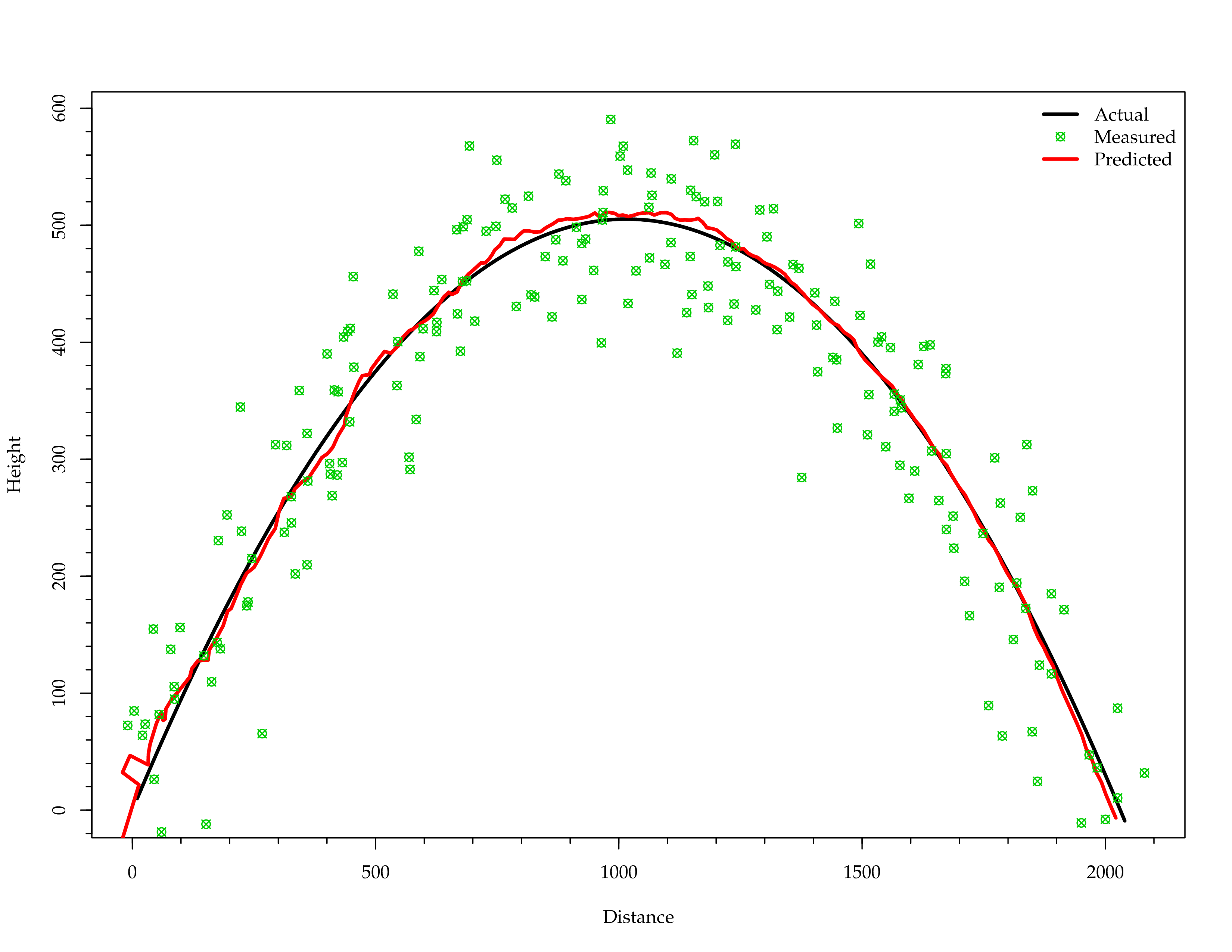
Example: Canon Ball

  val dt = 0.1
  val g = 9.8
  def I = DenseMatrix.eye[Double](4)

  val B = DenseMatrix(
    (0.0, 0.0, 0.0, 0.0),
    (0.0, 0.0, 0.0, 0.0),
    (0.0, 0.0, -1.0, 0.0),
    (0.0, 0.0, 0.0, -1.0)
  )
  val u = DenseVector(0, 0, g * Δt * Δt, g * Δt)
  val F = DenseMatrix(
    (1.0, dt,  0.0, 0.0),
    (0.0, 1.0, 0.0, 0.0),
    (0.0, 0.0, 1.0, dt),
    (0.0, 0.0, 0.0, 1.0)
  )
  val H = I
  val Q = DenseMatrix.zeros[Double](4, 4)
  val R = I * 0.2

  // guess of state and variance
  var s = DenseVector.zeros[Double](4)
  var P = I

  while (x(2) >= 0) {
    // measurement
    def noisy(actual: Double) = actual + Random.nextGaussian * 50
    val z = x.mapValues(noisy)

    // actual simulation
    x = F * x + B * u
    t += dt

    // prediction step
    val predS = F * s + B * u
    val predP = F * P * F.t + Q
    // observation step
    val innov = z - H * predS
    val innov_cov = H * predP * H.t + R
    // update step
    val gain = predP * H.t * inv(innov_cov)
    s = predS + gain * innov
    P = (I - gain * H) * predP
  }

Example: PCA

  val jpg = ImageIO.read(file("input.jpg"))
  val orig = imageToMatrix(jpg)

  val svd.SVD(u, s, v) = svd(orig)

  for {
    i <- 1 until u.cols
    if i <= 100 // no discernable difference beyond!
  } {
    val compressed = u(::, 0 until i) * diag(s(0 until i)) * v(0 until i, ::)

    val out = f"compressed-$i%03d.bmp"
    val converted = matrixToImage(compressed)
    ImageIO.write(converted, "BMP", file(out))
  }

Name	Vector	Matrix
1-norm	\(\Vert x\Vert _{1} = \sum_i \vert x_i\vert\)	\(\Vert A\Vert _{1} = \max_j \sum_i \vert a_{ij}\vert\)
2-norm	\(\Vert x\Vert _2 = ( \sum_i \vert x_i\vert^2 )^{1/2}\)	\(\Vert A\Vert _2 = \max_{x \neq 0} \Vert Ax\Vert _2 / \Vert x\Vert _2\)
Frobenius	\(\Vert x \Vert_F = \Vert x \Vert_2\)	\(\Vert A\Vert _F = ( \sum_{ij} \vert a_{ij}\vert^2 )^{1/2}\)
\(\infty\) norm	\(\Vert x\Vert _{\infty} = \max_i \vert x_i\vert\)	\(\Vert A\Vert _{\infty} = \max_i \sum_j \vert a_{ij}\vert\)

Level	Name	Operation
1	`xAXPY`	\(y \leftarrow \alpha x + y\)
1	`xDOT`	\(dot \leftarrow x^T y\)
1	...
2	`xGEMV`	\(y \leftarrow \alpha A x + \beta y\)
2	`xTRSV`	\(T \boldsymbol x = y\)
2	...
3	`xGEMM`	\(C \leftarrow \alpha A B + \beta C\)
3	`xTRSM`	\(T \boldsymbol B = \alpha \boldsymbol B\)
3	...

High Performance Linear Algebra

Sam Halliday

Scala eXchange December 2014

TL;DR

Linear Algebra

Definition

Diagonalisation

Example: Kalman Filter

Example: PCA

SVD

Basic Implementation

Multiplication

Immutable

Naive

Naive Parallel

Allocation

While Loops

Comparison

NETLIB

netlib.org

BLAS

Reference DGEMM

LAPACK

DGETRF

Optional: Solving with LU

C API

Precision and Stability

Kinds of Error

Types of Structures

Relative Errors

Norms

Condition Number

Example

Hardware Support

Bottleneck

Read and Write

Timings

CPU Architecture

CPU Cycles

Latency

Machine Optimised

Intel

Parallel Studio

MKL Standalone

AMD Core Math Library

Apple vecLib / Accelerate

ATLAS

GotoBLAS / OpenBLAS

DGEMM Benchmarks

DGEMM Comparison

netlib-java

Fortran to ...

... Java

API Generator

Regex Digression

Implementations

F2jBLAS

NativeRefBLAS and NativeSystemBLAS

JNI

Maven Native

JNILoader

Performance

Scala API

Breeze

Example: Canon Ball

Example: PCA

Hardware Acceleration

Graphics Cards (GPU)

FPGA

APU